EP2-Team/angabe/Teamaufgabe.md

Teamaufgabe (Aufgabenblatt 7)

Allgemeine Anmerkungen

Die Teamaufgabe (entspricht Aufgabenblatt 7) ist eine im Vergleich zu den anderen Aufgabenblättern etwas größere Programmieraufgabe, die in einem Zweierteam zu lösen ist. Rechtzeitig vor der Deadline soll Feedback zu einer vorläufigen Version der Lösung bei der betreuenden Tutorin oder dem betreuenden Tutor eingeholt werden (nötigenfalls auch mehrfach), und gegebene Empfehlungen sind in die Endversion einzuarbeiten.

Bitte beachten Sie, dass Sie maximal 12 der insgesamt 23 Punkte für die Teamaufgabe bekommen können, wenn Sie vorab kein Feedback einholen (siehe Punkteaufteilung ganz unten).

Deadlines:

• 23.05.2022: spätester Abgabetermin für das Einholen von Feedback
• 08.06.2022: finale Abgabe

Thema

In der Simulation von Aufgabenblatt 1 treten nur relativ wenige Himmelskörper auf. Die algorithmischen Kosten zur Berechnung der nächsten Position sind dabei quadratisch in n, das heißt, O(n²), wobei n die Anzahl der Himmelskörper in der Simulation ist. Das liegt daran, dass alle n(n-1)/2 Paare von Himmelskörpern gebildet werden müssen, um deren wechselseitige Gravitation und folglich die neue Position aller Himmelskörper berechnen zu können:

  // for each body (with index i): compute the total force exerted on it.
  for (int i = 0; i < bodies.length; i++) {
      forceOnBody[i] = new Vector3(); // begin with zero
      for (int j = 0; j < bodies.length; j++) {
          if (i != j) {
              Vector3 forceToAdd = gravitationalForce(bodies[i], bodies[j]);
              forceOnBody[i] = plus(forceOnBody[i], forceToAdd);
          }
      }
  }
  // now forceOnBody[i] holds the force vector exerted on body with index i.

Codebeispiel 1: verschachtelte Schleifen in der Methode main der Klasse Simulation in Aufgabenblatt 1.

Ziel dieser Teamaufgabe ist es, die algorithmischen Kosten durch Verwendung eines Näherungsverfahrens zu reduzieren: Grundlage ist der Barnes-Hut-Algorithmus [1], mit dem alle wechselseitigen Gravitationskräfte mit einem geringeren Aufwand von O(n*log(n)) angenähert werden können.

Bei einer richtigen Umsetzung können Sie in Ihrer Simulation in der Folge eine wesentlich größere Anzahl von Himmelskörpern verwenden und damit auch Sternhaufen oder Galaxien simulieren.

Der Barnes-Hut-Algorithmus

Der Trick des Barnes-Hut-Algorithmus ist, Gruppen von Himmelskörpern, die relativ nahe beisammen liegen, zusammenzufassen. Beinhaltet eine solche Gruppe m Himmelskörper und ist die Gesamtmasse der Gruppe (Summe aller Massen) und der Schwerpunkt der Gruppe (mit Massen gewichteter Mittelwert aller Positionen) bereits berechnet worden, lässt sich die Wirkung der Gruppe auf einen entfernten Himmelskörper (der nicht Teil der Gruppe ist) in einem Schritt, anstatt in m Schritten berechnen.

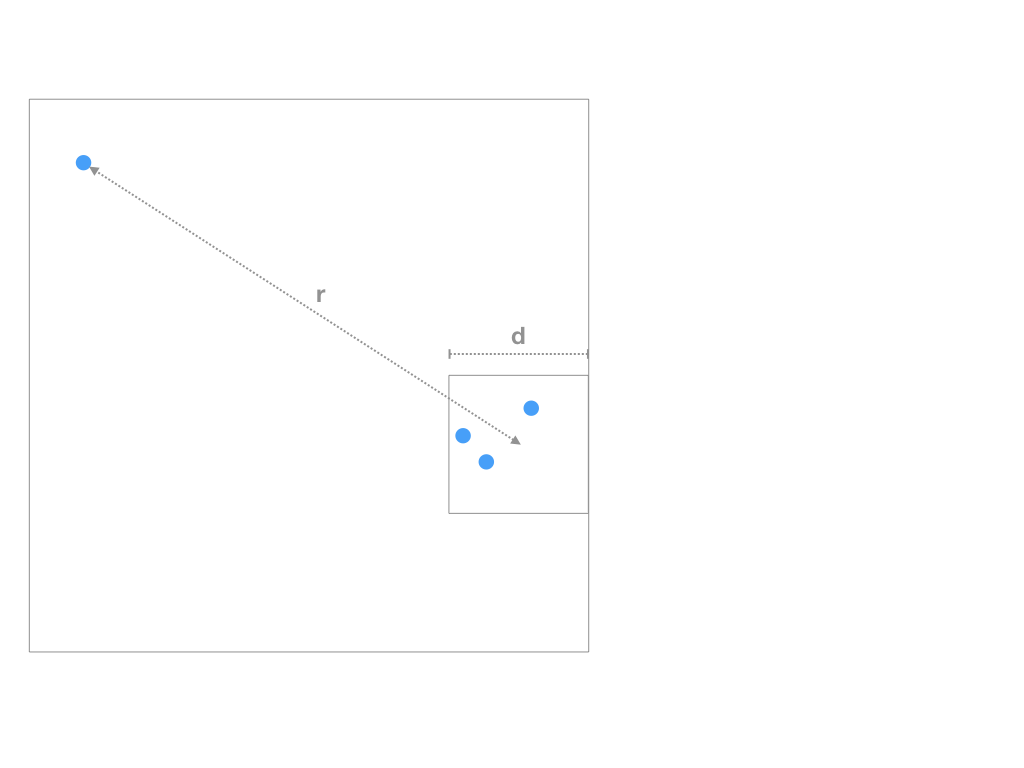
Diese Beschleunigung hat jedoch einen Preis: die Berechnung stimmt nur näherungsweise. Liegt der Himmelskörper (z.B. unsere Sonne) jedoch weit genug von einer Gruppe (z.B. Andromedagalaxie) entfernt, ist der Fehler der Annäherung zu vernachlässigen. Die Entfernung r zur Gruppe muss zum Durchmesser d der Gruppe in einem bestimmten Verhältnis stehen. Dieses wird mit einem spezifizierten Schwellwert T festgelegt. Um die Gruppe zusammenzufassen, muss gelten d/r < T (siehe Abbildung 1).

Abbildung 1: Wenn ein einzelner Himmelskörper von einer Gruppe von Himmelskörpern weit genug entfernt ist, kann die Kraft, die von der Gruppe auf den einzelnen Himmelskörper wirkt, schneller berechnet werden. Gruppen entsprechen Teilbäumen, das heißt, (Unter-) Quadranten mit Seitenlänge d. Die Genauigkeit der Näherung ist ausreichend, falls d/r < T, wobei r die Distanz vom Himmelskörper zum Mittelpunkt des Quadranten und T ein spezifizierter Schwellwert ist, mit dem die Genauigkeit der Simulation eingestellt werden kann. In der Literatur wird häufig T = 1 gesetzt.

Datenstruktur: Octree

Wie werden nun die Gruppen gefunden, die man zusammenfassen kann? Eine geeignete Datenstruktur ist der Quadtree in 2D bzw. der Octree in 3D. Wir werden die Konzepte anhand des Quadtrees darstellen, in Ihrer Lösung sollen Sie dann aber einen Octree verwenden, da die Himmelskörper im 3D-Raum liegen:

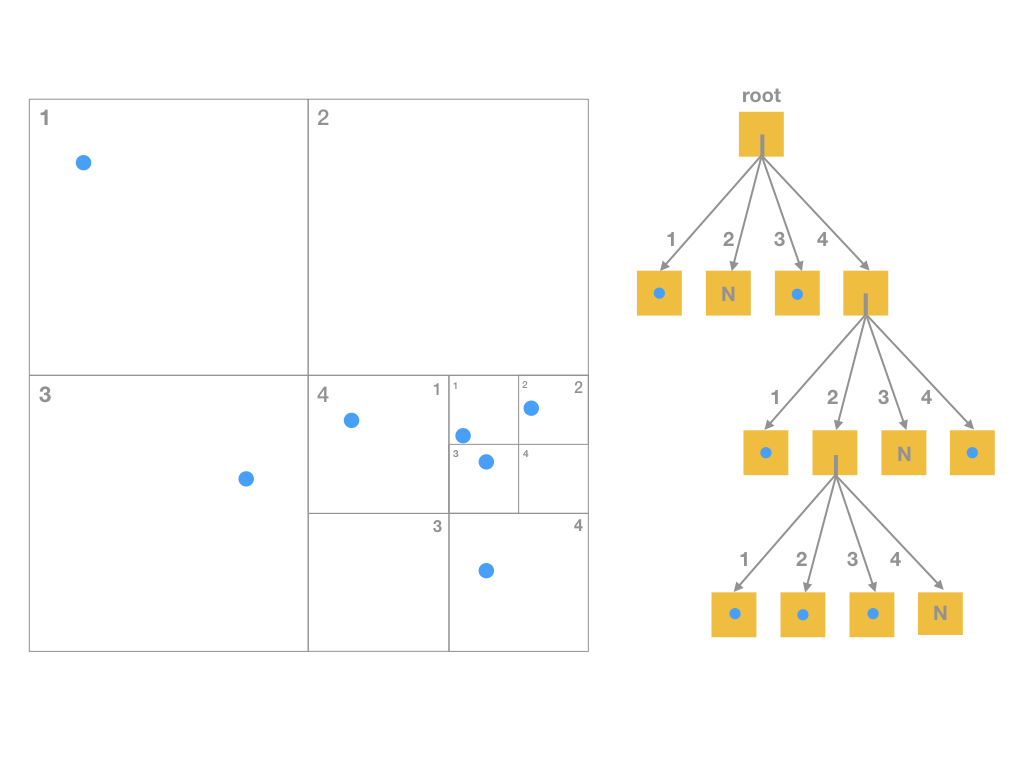
1. Der erste Schritt ist, alle Himmelskörper der Simulation in eine Baumstruktur (den Quadtree bzw. Octree) einzufügen. Das Einfügen geschieht rekursiv: Ist ein Knoten leer (null), wird der Himmelskörper eingefügt und es entsteht dabei ein Blattknoten, der genau einen Himmelskörper enthält. Ist der Knoten, in den eingefügt wird, ein Blattknoten mit genau einem Himmelskörper, wird der Blattknoten in vier - zunächst leere - Quadranten geteilt und beide Himmelskörper in die entsprechenden Quadranten eingefügt. Jeder Quadrant entspricht einem Unterbaum (siehe Abbildung 2). Zur Vermeidung mehrfacher Berechnungen sollte jeder Knoten (auf jeder Ebene des Baumes) Gesamtmasse und Schwerpunkt der enthaltenen Himmelskörper speichern. Die Größen werden beim Einfügen aktualisiert. Recherchieren Sie ggfs. die Details einer Quadtree-Implementierung.

2. Berechnung der Schwerkraft: Für jeden Himmelskörper (hier kann ein Iterator über alle Elemente des Baums genutzt werden) wird die auf ihn wirkende Kraft berechnet. Dabei wird die Baumstruktur ausgenutzt. Für Teilbäume, deren Quadranten die in Abbildung 1 beschriebenen Eigenschaften erfüllen, das heißt, vom Himmelskörper weit genug entfernt sind, kann die Kraft, die vom Quadranten ausgeht, ermittelt werden, ohne den Baum weiter hinab steigen zu müssen. Es wird also beim Traversieren des Baumes getestet, ob ein Quadrant die Eigenschaft erfüllt. Ist das nicht der Fall, werden - solange es noch welche gibt - alle Unterquadranten geprüft, im ungünstigsten Fall bis zu den Blattknoten. Das bedeutet, dass man für T = 0 die gleiche Lösung bekommt, wie bei der direkten Aufsummierung aller Kräfte (aufgrund der Verwaltung der Daten durch den Baum jedoch noch langsamer).

3. Nachdem alle Himmelskörper gemäß der auf sie wirkenden Kräfte bewegt wurden, muss der gesamte Baum neu aufgebaut werden, das heißt, Punkt 1 und 2 werden in der Simulation in einer Schleife wiederholt.

Abbildung 2: Sieben Himmelskörper und der entsprechende Quadtree: Blattknoten sind entweder null (N in der Abbildung) oder beinhalten genau einen Himmelskörper. Knoten, die nicht Blattknoten sind, haben vier Nachfolgerknoten, die vier (Unter-)quadranten repräsentieren. Im Fall eines Octrees in 3D sind es acht Oktanten (Würfelregionen).

Aufgabe

Setzen Sie den Barnes-Hut-Algorithmus um, ohne dabei mögliche Kollisionen von Himmelskörpern zu berücksichtigen (siehe freiwillige Zusatzaufgabe).

Entwerfen und implementieren Sie neue Klassen, die die verlangte Datenstruktur abbilden. Nutzen Sie dafür die geeigneten Sprachmittel aus der Vorlesung. Erstellen Sie neue Versionen ihrer bestehenden Klassen, sodass der oben beschriebene Algorithmus integriert werden kann. Die meisten der zur Lösung benötigten Konzepte werden erst in kommenden Vorlesungseinheiten besprochen. Insbesondere das Kapitel 3 des Skriptums ist für die Erstellung der Lösung hilfreich.

Sie können die Form der grafischen Darstellung selbst auswählen. Der dargestellte Ausschnitt sollte die gesamte Region, die vom Octree abgedeckt wird, darstellen. Sie können eine Projektionsrichtung für die Visualisierung wählen (z.B. wie bisher Projektionen auf die x-y-Ebene).

Hinweise zum Testen: Zwecks Vergleichbarkeit, testen Sie die Simulation zunächst mit den Himmelskörpern, die Sie in bisherigen Versionen benutzt haben. Eine weitere Möglichkeit zu testen ist, zunächst alle z-Koordinaten auf 0 zu setzen und auch die Regionen der Blattknoten zu visualisieren (siehe Abbildung 4).

Generieren Sie unter Verwendung von Zufallszahlgeneratoren eine große Anzahl n von Himmelskörpern unterschiedlicher Massen und initialen Positionen und Bewegungsvektoren. Hier müssen Sie durch Ausprobieren eine brauchbare Initialisierung der Simulation finden. Sie können auch mehrere Sternhaufen an verschiedenen Positionen erzeugen und/oder einzelne sehr massenreiche Objekte (schwarze Löcher) einfügen. n und T sollten jedenfalls spezifizierbar sein oder zu Beginn eingegeben werden. Sie sollten n mindestens auf 10000 setzen. Ihre Simulation sollte so effizient sein, dass dabei deutliche Bewegungsmuster erkennbar sind und eine deutliche Laufzeitverbesserung im Vergleich zum Fall T=0 erkennbar ist. Testen Sie auch, wie die Laufzeit und die Simulation sich für verschiedene Werte von T verhält. Ein Beispiel einer Simulation ist in Abbildung 3 dargestellt.

Sie werden ein Phänomen beobachten, das auch in der Realität auftritt: Manchmal werden Sterne aus einem Sternhaufen herausgeschleudert. Auch in der Simulation werden hin und wieder Himmelskörper so stark beschleunigt, dass sie den beobachteten Ausschnitt, also die mit dem Wurzelknoten assoziierte Region, verlassen. Diese Himmelskörper können in der nächsten Iteration nicht mehr in den Baum übernommen werden. Dadurch verkleinert sich die Anzahl der Himmelskörper in der Simulation im Lauf der Zeit.

Behandlung von Kollisionen (freiwillig)

Sie können Ihren Octree so erweiteren, dass beim Einfügen eines Himmelskörpers überprüft wird, ob es dabei zu Kollisionen kommt. Falls das so ist, sollten die entsprechenden Himmelskörper gleich verschmolzen werden. Dabei sollte der Octree ausgenutzt werden, sodass möglichst wenige Kollisionsüberprüfungen durchgeführt werden und das Einfügen effizient bleibt.

Dazu überprüft man beim Einfügen nur jene Knoten, die sich mit dem einzufügenden Himmelskörper überschneiden. Dabei geht man rekursiv vor bis man für Kinderknoten einen Blattknoten erreicht. Dann führt man eine Kollisionsprüfung zwischen dem Himmelskörper dieses Blattknotens und dem Himmelskörper, den man einfügt, durch.

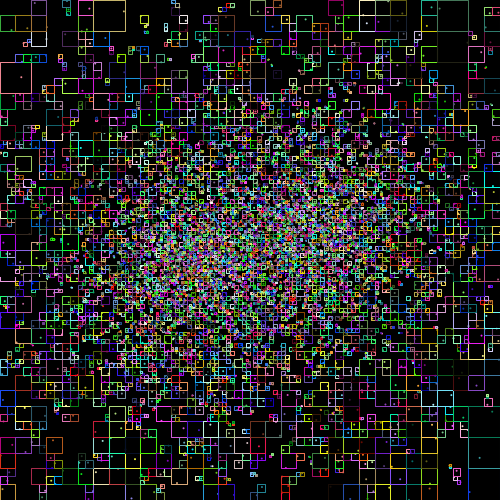Abbildung 3: Eine Simulation mit 10000 Himmelskörpern.	Abbildung 4: Die Simulation mit Darstellung der Quadranten von nicht-leeren Blattknoten.

[1] J. Barnes und P. Hut: ''A hierarchical O(N log N) force-calculation algorithm'' in Nature, 324:446-449, 1986 (kann im TU VPN heruntergeladen werden).

Punkteaufteilung

• Aufbau Octree: 8 Punkte
• Berechnung wechselseitiger Schwerkraft im Octree : 9 Punkte
• Simulation mit grafischer Ausgabe: 6 Punkte

Gesamt: 23 Punkte

Hinweis: wenn vor der Abgabe kein Feedback von einer Tutorin oder einem Tutor eingeholt wurde, sind maximal 12 Punkte erreichbar.